The Sun provides warmth and light that is essential for life on Earth. But have you ever wondered what powers this immense ball of fire? The answer lies in nuclear fusion, a process that occurs deep within the core of the Sun and other stars, where lighter atomic nuclei combine to form heavier nuclei, releasing vast amounts of energy in the process. In this lesson, we’ll explore how nuclear fusion works, the different types of fusion reactions in stars, and how these reactions shape the life cycles of stars and contribute to the formation of elements in the universe.

What is Nuclear Fusion?

Nuclear fusion is the process by which two light atomic nuclei combine to form a heavier nucleus, releasing energy in the process. This reaction is the primary energy source for stars, including our Sun.

Conditions for Fusion: For nuclear fusion to occur, the nuclei must overcome their natural repulsion due to their positive charges. This requires extremely high temperatures (millions of degrees) and pressures, which are found in the cores of stars. The immense gravitational force in a star’s core compresses the gas to such an extent that the temperature rises high enough to allow fusion to occur.

Did You Know? The Sun’s core temperature is around 15 million degrees Celsius, a condition necessary for hydrogen nuclei to fuse into helium.

The Proton-Proton Chain Reaction

The proton-proton (p-p) chain is the dominant fusion process in stars the size of the Sun. It involves a series of reactions where hydrogen nuclei (protons) combine to form helium, releasing energy at each step.

Step-by-Step Process:

1. Step 1: Formation of Deuterium
   • Two protons collide at high speeds. Normally, they would repel each other due to their positive charges, but under the extreme conditions in a star’s core, one proton undergoes beta decay and converts into a neutron. This forms Deuterium (Hydrogen-2), consisting of one proton and one neutron.
   • Reaction: The first step involves the fusion of two protons ($^1\text{H}$) to form deuterium ($^2\text{H}$), releasing a positron ($e^+$) and a neutrino ($\nu_e$).

     \[^1\text{H} + ^1\text{H} \rightarrow ^2\text{H} + e^+ + \nu_e\]

Here, the superscripts indicate the total number of protons and neutrons in the nucleus.

• Time Scale: This step is the slowest, taking about a billion years on average for a proton in the Sun.

1. Step 2: Formation of Helium-3
   • The newly formed Deuterium nucleus collides with another proton, resulting in the formation of Helium-3 (two protons and one neutron).
   • Reaction: In the second step, the deuterium nucleus ($^2\text{H}$) produced in the first step fuses with another proton to form helium-3 ($^3\text{He}$), releasing a gamma-ray photon.

     \[^2\text{H} + ^1\text{H} \rightarrow ^3\text{He} + \gamma\]

   • Time Scale: This reaction happens quickly, in about 4 seconds.

1. Step 3: Formation of Helium-4
   • Finally, two Helium-3 nuclei collide to form Helium-4 (two protons and two neutrons) and release two protons.
   • Reaction: The third step involves the fusion of two helium-3 nuclei ($^3\text{He}$) to form helium-4 ($^4\text{He}$) and two protons.

     \[^3\text{He} + ^3\text{He} \rightarrow ^4\text{He} + ^1\text{H} + ^1\text{H}\]

   • Time Scale: This step takes about 400 years for Helium-3 nuclei to collide in the Sun’s core.

Note:

The third step requires two helium-3 nuclei to start; the first two steps must happen twice before the third step can occur.

Proton-Proton Chain Summary:

The proton-proton chain converts four hydrogen nuclei into one helium nucleus, releasing energy in the form of light and heat. This energy is what powers the Sun and provides the warmth and light we receive on Earth.

Energy Generation in the Proton-Proton (p-p) Chain

In the proton-proton (p-p) chain, four hydrogen nuclei (protons) are ultimately fused to form a single helium-4 nucleus. The overall reaction can be represented as:

\[^1\text{H} + ^1\text{H} + ^1\text{H} + ^1\text{H} \rightarrow ^4\text{He} + 2e^+ + 2\nu_e + 2\gamma + \text{energy}\]

To determine the amount of energy released during this process, we can calculate the difference in mass between the initial hydrogen atoms and the final helium atom. The mass of a hydrogen atom is 1.007825 atomic mass units (u), and the mass of a helium-4 atom is 4.00268 u. Here, we use the full atomic mass, including electrons, because the process involves the creation and annihilation of positrons and electrons.

The mass of the initial four hydrogen atoms is:

\[4 \times 1.007825 \, \text{u} = 4.03130 \, \text{u}\]

The mass of the final helium atom is:

\[4.00268 \, \text{u}\]

The difference in mass, which is converted to energy, is:

\[4.03130 \, \text{u} - 4.00268 \, \text{u} = 0.02862 \, \text{u}\]

Using Einstein’s mass-energy equivalence formula, $E = mc^2$, where $c$ is the speed of light ($3 \times 10^8$ meters per second), the energy released by this mass conversion is:

\[E = 0.0071 \, \text{kg} \times \left(3 \times 10^8 \, \text{m/s}\right)^2 = 6.4 \times 10^{14} \, \text{J}\]

This amount of energy, released from the fusion of just 1 kilogram of hydrogen, is enough to supply all the electricity used in the United States for approximately two weeks.

The Sun, which shines with a luminosity of $4 \times 10^{26}$ watts, must fuse about 600 million tons of hydrogen into helium every second to maintain its brightness. Of this, around 4 million tons of mass are converted directly into energy. Despite the enormous quantities involved, the Sun has such a vast reserve of hydrogen that it can continue this fusion process for billions of years, ensuring its place as our solar system’s energy source for a long time to come.

The CNO Cycle

In stars more massive than the Sun, the Carbon-Nitrogen-Oxygen (CNO) cycle dominates as the primary fusion process. While it still converts hydrogen into helium, it uses carbon, nitrogen, and oxygen as catalysts.

Overview:

• The CNO cycle involves the fusion of hydrogen nuclei with carbon, nitrogen, and oxygen, leading to the formation of helium. These heavier elements act as catalysts and are not consumed in the reaction.
• Energy Released: The CNO cycle releases more energy per cycle than the proton-proton chain, which is why it is more prevalent in hotter, more massive stars.

Comparison with Proton-Proton Chain:

• Temperature Dependence: The CNO cycle requires a higher core temperature than the proton-proton chain, which is why it is more efficient in more massive stars.
• Role in Star Types: The proton-proton chain is dominant in stars with a mass similar to or smaller than the Sun, while the CNO cycle is dominant in larger stars.

Energy Transport in Stars

The energy produced by nuclear fusion in the core of a star must journey to the star’s surface before it can be radiated into space as light and heat. This energy travels through various layers of the star, each with unique properties that influence how energy is transferred.

Radiative Zone:

• In the radiative zone, energy is transported outward by radiation. Here, photons are absorbed and re-emitted by particles, slowly making their way from the hot core to cooler outer regions. This process is incredibly slow—each photon may take thousands of years to reach the next layer because it constantly interacts with particles, zigzagging through the dense material of the star. The radiative zone acts like a dense forest, where light must weave its way through countless obstacles.
• The radiative zone is more prominent in stars like the Sun, where the energy from the core is primarily transferred by this slow but steady process.

Convection Zone:

• Above the radiative zone lies the convection zone, where the mode of energy transfer changes dramatically. In this region, the energy causes hot plasma to rise toward the star’s surface, cool down, and then sink back toward the interior to be reheated—a process known as convection. This is similar to the way boiling water circulates in a pot. The convective zone is turbulent and dynamic, with massive currents of hot gas churning beneath the star’s surface.
• Convection is particularly important in cooler stars, where the outer layers are less efficient at radiating energy. In these stars, the convective zone can extend much deeper, playing a crucial role in energy transport.

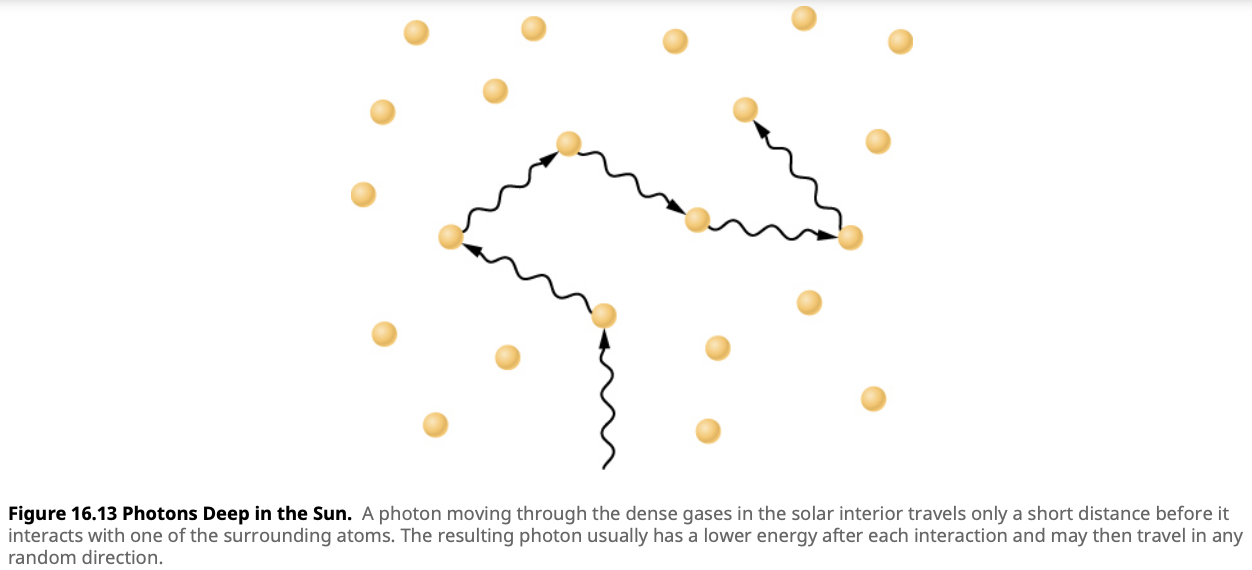
Nuclear Fusion and Star Life Cycles

Nuclear fusion is not only the engine that powers stars; it also shapes their entire life cycle, from their stable years on the main sequence to their dramatic ends.

The Role of Fusion in Stellar Evolution:

• Main Sequence Stars:
  • Stars begin their lives on the main sequence, where they spend the majority of their existence fusing hydrogen into helium in their cores. This fusion provides the energy that counteracts gravity, keeping the star stable. The balance between the outward pressure from fusion and the inward pull of gravity is what maintains a star’s equilibrium.
  • During this phase, a star’s mass determines its brightness and color. More massive stars burn hotter and brighter but have shorter lifespans, while less massive stars burn cooler and dimmer, living much longer.

• Post-Main Sequence:
  • As stars exhaust their hydrogen fuel, the core contracts and heats up, leading to the fusion of helium and other heavier elements. This marks the beginning of the post-main sequence phase. For stars like the Sun, this transition turns them into red giants, where their outer layers expand and cool, giving the star a reddish appearance.
  • More massive stars continue to fuse heavier elements in their cores, moving through stages of carbon, oxygen, and even silicon fusion. Each new stage of fusion occurs at increasingly higher temperatures and lasts for shorter periods of time.

Helium Burning and Beyond:

• Red Giants and Supergiants:
  • In stars like the Sun, once hydrogen is depleted, helium fusion begins, leading to the formation of carbon and oxygen. This helium burning phase causes the star to expand into a red giant. Eventually, the outer layers may be ejected into space, creating a planetary nebula, while the core remains as a white dwarf.
  • In more massive stars, after helium is used up, the core contracts further, and fusion of heavier elements like carbon and oxygen begins. These stars become supergiants, with a layered structure resembling an onion, where each layer is fusing different elements.
• The Final Act—Supernovae and Stellar Remnants:
  • When massive stars reach the point where their cores are made of iron, fusion can no longer produce energy. This leads to a catastrophic core collapse, resulting in a supernova explosion. This explosion scatters heavy elements into space, contributing to the cosmic material that forms new stars and planets.
  • The remnants of the explosion depend on the mass of the core:
    • White Dwarf: For smaller stars, the remnant is a white dwarf, which slowly cools over time.
    • Neutron Star: In more massive stars, the core collapse leads to the formation of a neutron star, an incredibly dense object composed mostly of neutrons.
    • Black Hole: If the star is massive enough, the core continues collapsing to form a black hole, an object with gravity so strong that not even light can escape.

Check Your Understanding

1. Proton-Proton Chain: Describe the steps involved in the proton-proton chain reaction in stars like the Sun. Why is the first step the slowest?
   
   

2. Energy Transport: Explain how energy is transported from the core of the Sun to its surface. Why does this process take so long?
   
   

3. Stellar Nucleosynthesis: How does nucleosynthesis in stars contribute to the formation of elements in the universe? Why are supernovae important for element distribution?
   
   

4. Energy Released in Fusion: Calculate the energy released when a proton combines with a deuterium nucleus to form helium-3 ($^3\text{He}$). Use the following atomic masses: $^1\text{H} = 1.007825 \, \text{u}$, $^2\text{H} = 2.014102 \, \text{u}$, and $^3\text{He} = 3.016029 \, \text{u}$. Apply Einstein’s equation $E = mc^2$, where $c = 3 \times 10^8 \, \text{m/s}$, and note that 1 u = $1.66054 \times 10^{-27}$ kg.
   
   

5. Energy Conversion Over Time: The Sun converts $4 \times 10^9$ kg of mass to energy every second. How many years would it take the Sun to convert a mass equal to the mass of Earth ($6 \times 10^{24}$ kg) to energy?
   
   

6. Total Energy Potential of the Sun: Assume that the Sun’s mass is 75% hydrogen and that all of this mass could be converted to energy according to Einstein’s equation $E = mc^2$. The mass of the Sun is $2 \times 10^{30}$ kg. How much total energy could the Sun generate? Express your answer in joules.
   
   

7. Total Energy from Solar Hydrogen: If all the hydrogen atoms in the Sun were converted into helium, how much total energy would be produced? Estimate the total number of hydrogen atoms in the Sun, considering that hydrogen constitutes 75% of the Sun’s mass. (Hint: The mass of one hydrogen atom is approximately $1.67 \times 10^{-27}$ kg.)
   
   

8. Sun’s Mass Reduction Over Time: The Sun converts 4 million tons of matter into energy every second. How long will it take for the Sun to reduce its mass by 1%? Compare your result with the Sun’s current age of approximately 4.6 billion years. The mass of the Sun is $2 \times 10^{30}$ kg.
   
   

Resources

• Astronomy (2016). Andrew Fraknoi, David Morrison, and Sidney C. Wolff.
• Foundations of Astrophysics (2010). Barbara Ryden and Bradley M. Peterson.