Introduction
Today we will uncover the story of Kepler’s Laws of Planetary Motion. These laws revolutionized our understanding of the solar system and laid the foundation for modern astronomy.
Video
Watch this video for an overview of Kepler's Laws of Planetary Motion.
Historical Context
Johannes Kepler: The Mathematician of the Heavens
Johannes Kepler was a German mathematician and astronomer who lived in the late 16th and early 17th centuries. Born in 1571, Kepler is best known for formulating the three laws of planetary motion, which described the orbits of planets around the Sun with unprecedented accuracy.
Tycho Brahe: The Observational Genius
Tycho Brahe, a Danish nobleman, was a meticulous observer of the stars and planets. His detailed astronomical data provided the foundation upon which Kepler built his laws. Brahe’s observations were the most accurate of his time, and his collaboration with Kepler was crucial to the development of the laws of planetary motion.
The Copernican Revolution
The heliocentric model proposed by Nicolaus Copernicus placed the Sun at the center of the solar system, challenging the long-held geocentric model. Kepler’s laws provided the mathematical evidence needed to support Copernicus’s revolutionary idea, cementing the heliocentric model as the correct representation of our solar system.
Kepler’s Laws of Planetary Motion
First Law (Law of Ellipses)
Imagine a time when the prevailing belief was that planets orbited the Earth in perfect circles. This view dominated until Johannes Kepler, through meticulous analysis of Tycho Brahe’s precise observations, discovered something remarkable. Kepler found that the planets, including our Earth, do not travel in perfect circles but rather in ellipses—an elegant, stretched circle.
Kepler’s First Law states that planets move in elliptical orbits with the Sun at one focus.
An ellipse has a unique shape characterized by two focal points (foci). For planetary orbits, one of these foci is occupied by the Sun. The degree of this “stretching” is determined by the eccentricity of the ellipse. An eccentricity of 0 indicates a perfect circle, while values approaching 1 indicate increasingly elongated shapes. This breakthrough explained the varying distances between the planets and the Sun, a phenomenon that could not be reconciled with circular orbits.
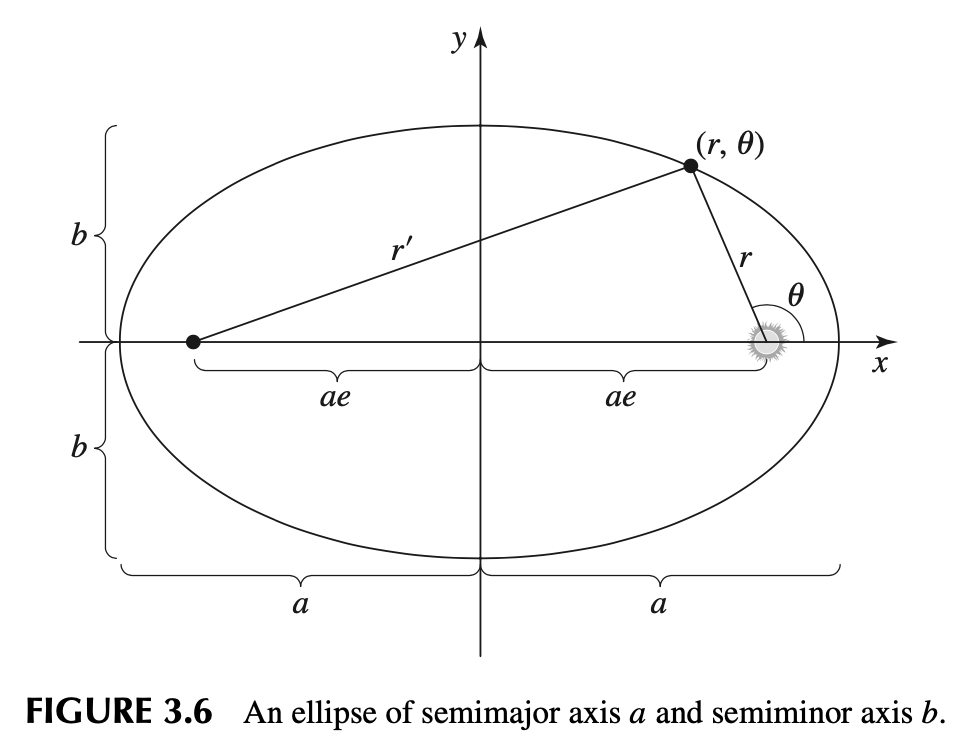
Kepler’s First Law shattered the long-held notion of circular orbits and paved the way for a deeper understanding of celestial mechanics. It was a testament to the power of careful observation and the willingness to challenge established beliefs.
Second Law (Law of Equal Areas)
Kepler found that, when a planet was moving along its elliptical path, it accelerated as it got closer to the Sun, covering a greater distance in a shorter time. Conversely, when it was further away from the Sun, it slowed down. Kepler’s Second Law captures this beautifully by asserting that the imaginary line connecting a planet to the Sun sweeps out equal areas in equal time periods, regardless of where the planet is in its orbit.
Kepler’s Second Law states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
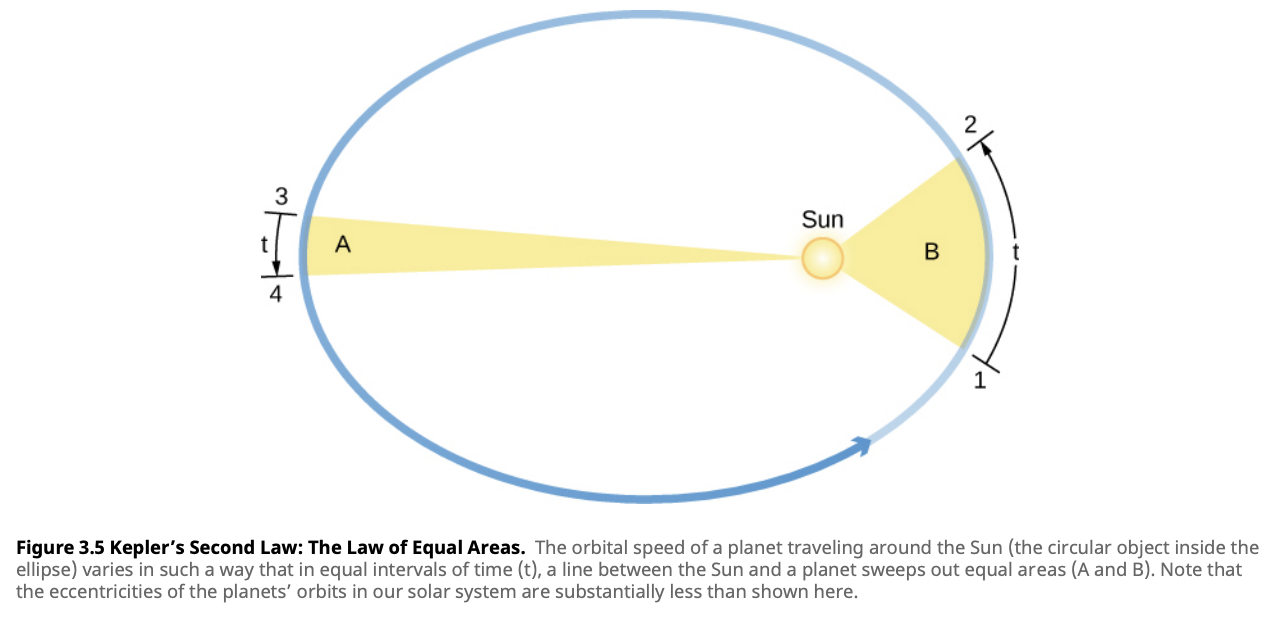
For instance, when Earth is at perihelion (the point closest to the Sun), it travels faster, zipping through its orbit. When it reaches aphelion (the point farthest from the Sun), its pace slows. This variation in speed explained why planets appeared to change their velocity as observed from Earth—an observation that had puzzled astronomers for centuries.
Kepler’s Second Law not only provided insights into planetary motion but also hinted at the gravitational forces at play, a concept that would later be fully developed by Sir Isaac Newton.
Third Law (Law of Harmonies)
Kepler also found that there is a precise mathematical relationship between the time a planet takes to orbit the Sun (its orbital period) and the size of its orbit (the semi-major axis). Specifically, the square of a planet’s orbital period is proportional to the cube of the semi-major axis of its orbit.
Kepler’s Third Law states that the square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
Mathematically, this can be written as:
\[P^2 \propto a^3\]
or
\[P^2 = k \cdot a^3\]
where $ P $ is the orbital period, $ a $ is the semi-major axis, and $ k $ is a constant.
To put this in perspective, consider Earth and Mars. Earth, with a semi-major axis of 1 astronomical unit (AU), completes an orbit in one year. Mars, with a semi-major axis of about 1.52 AU, takes approximately 1.88 Earth years to complete its orbit. Plugging these values into Kepler’s formula, we find that:
\(P_{\text{Earth}}^2 = 1^2 = 1\) \(a_{\text{Earth}}^3 = 1^3 = 1\)
\(P_{\text{Mars}}^2 \approx 1.88^2 = 3.53\) \(a_{\text{Mars}}^3 \approx 1.52^3 = 3.52\)
This near-perfect correlation between $ P^2 $ and $ a^3 $ demonstrated the universal applicability of Kepler’s Third Law across different planets, from Mercury to the distant gas giants.
Kepler’s Third Law unified the celestial mechanics of our solar system, offering a powerful tool for predicting planetary positions and understanding the vast cosmic clockwork. It set the stage for Newton’s laws of motion and universal gravitation, which would further explain the forces driving these harmonious motions.
Orbital Data for the Planets
To see Kepler’s laws in action, let’s examine the orbital data for the planets in our solar system:
| Planet | Semimajor Axis (AU) | Period (years) | Eccentricity |
|---|---|---|---|
| Mercury | 0.39 | 0.24 | 0.21 |
| Venus | 0.72 | 0.6 | 0.01 |
| Earth | 1.00 | 1.00 | 0.02 |
| Mars | 1.52 | 1.88 | 0.09 |
| (Ceres) | 2.77 | 4.6 | 0.08 |
| Jupiter | 5.20 | 11.86 | 0.05 |
| Saturn | 9.54 | 29.46 | 0.06 |
| Uranus | 19.19 | 84.01 | 0.05 |
| Neptune | 30.06 | 164.82 | 0.01 |
Mathematical Examples
Solution:
- Formula: Kepler’s Third Law relates the square of the orbital period ($P$) to the cube of the semimajor axis ($a$): \(P^2 = a^3\)
- Substitute the Given Value: $a = 50 \text{ AU}$ \(P^2 = 50^3\) \(P^2 = 125000\)
- Solve for $P$: \(P = \sqrt{125000}\) \(P \approx 353.55 \text{ years}\)
Therefore, the orbital period of an object with a semimajor axis of 50 AU is approximately 353.55 years.
Solution:
For Venus:
- Given: \(P = 0.62 \text{ years}, \quad a = 0.72 \text{ AU}\)
- Calculate $P^2$: \(P^2 = 0.62^2 \approx 0.3844\)
- Calculate $a^3$: \(a^3 = 0.72^3 \approx 0.3732\)
For Venus, $ P^2 \approx 0.3844 $ and $ a^3 \approx 0.3732 $.
For Earth:
- Given: \(P = 1.00 \text{ year}, \quad a = 1.00 \text{ AU}\)
- Calculate $P^2$: \(P^2 = 1.00^2 = 1.00\)
- Calculate $a^3$: \(a^3 = 1.00^3 = 1.00\)
For Earth, $ P^2 = 1.00 $ and $ a^3 = 1.00 $.
Applications and Implications
Predicting Planetary Positions
Kepler’s laws allow astronomers to predict the positions of planets in their orbits with great accuracy. This capability is crucial for space navigation and understanding the dynamics of our solar system.
In the early 17th century, predicting the precise locations of planets was an arduous task filled with inaccuracies. Before Kepler, astronomers relied on complex systems of epicycles and deferents to explain planetary motion, a method rooted in the Ptolemaic geocentric model. However, these systems often fell short in matching observations, leading to significant errors in predictions.
With the advent of Kepler’s laws, the process of predicting planetary positions became not only simpler but also far more precise. Kepler’s First Law clarified that planets travel in elliptical orbits, which accounted for the varying distances between planets and the Sun. His Second Law described how planets speed up and slow down in their orbits, allowing for accurate calculation of their velocities at any given point. The Third Law provided a direct relationship between a planet’s orbital period and the size of its orbit, making it possible to predict how long it takes for a planet to complete one revolution around the Sun.
Let’s consider the example of Mars, which was particularly puzzling to astronomers before Kepler. Using Tycho Brahe’s detailed observations, Kepler determined that Mars follows an elliptical path. By applying his laws, he could predict Mars’ position in the sky at any given time. This was a groundbreaking achievement that not only matched but also exceeded the accuracy of previous models.
Kepler’s Legacy in Modern Astronomy
Kepler’s laws are not confined to our solar system alone. They are used to study exoplanets—planets orbiting stars other than the Sun. By observing the dimming of a star as a planet passes in front of it (a method known as the transit method), astronomers can apply Kepler’s Third Law to determine the exoplanet’s orbital period and distance from its star. This has led to the discovery of thousands of exoplanets, expanding our understanding of the universe.
Historical Anecdote: Halley’s Comet
A fascinating historical application of Kepler’s laws involves Halley’s Comet. Edmond Halley, using Kepler’s laws, calculated the orbit of this famous comet and predicted its return in 1758. Although Halley did not live to see the comet’s return, his prediction proved accurate, solidifying the laws’ reliability in predicting celestial events. Halley’s Comet continues to be a testament to the enduring power of Kepler’s laws.
Conclusion
Kepler’s laws revolutionized our ability to predict planetary positions with unmatched precision. From guiding early astronomers to paving the way for modern space missions and the discovery of distant worlds, these laws are a cornerstone of our understanding of the cosmos. The accuracy and elegance of Kepler’s laws continue to inspire astronomers and scientists, driving humanity’s quest to explore and comprehend the vast universe.
Check Your Understanding
- According to Kepler’s second law, where in a planet’s orbit would it be moving fastest? Where would it be
moving slowest?
- Pluto’s orbit is more eccentric than any of the major planets. What does that mean?
- What is the average distance from the Sun (in astronomical units) of an asteroid with an orbital period of
8 years?
- In 1996, astronomers discovered an icy object beyond Pluto that was given the designation 1996 TL 66. It
has a semimajor axis of 84 AU. What is its orbital period according to Kepler’s third law?
Resources
- Astronomy (2016). Andrew Fraknoi, David Morrison, and Sidney C. Wolff.
- Foundations of Astrophysics (2010). Barbara Ryden and Bradley M. Peterson.