Introduction

Have you ever gazed up at the night sky and wondered why some stars shine brighter than others? The study of stellar brightness not only allows us to appreciate the beauty of the cosmos but also provides crucial information about the stars themselves. In this lesson, we’ll explore how astronomers measure the brightness of stars, the physics behind their luminosity, and the historical context of the magnitude scale.

Video

Watch this video for an excellent overview of the brightness of stars, including practical examples and historical context.

Flux and Luminosity

To understand stellar brightness, we first need to define a few key concepts: flux and luminosity.

Flux is the amount of light energy received per unit area per unit time. Imagine standing under a streetlamp at night. The light that hits you is the flux.

Luminosity, on the other hand, is the total amount of energy a star emits per unit time. Think of it as the star’s total power output.

The Inverse Square Law

As light travels from a star, it spreads out over an ever-increasing area. This spreading out follows the Inverse Square Law, which states that the flux decreases with the square of the distance from the source. Mathematically, we express this as:

\[F = \frac{L}{4\pi r^2}\]

where:

This law explains why stars appear dimmer the farther away they are. It’s not because they’re less powerful, but because their light spreads out over a larger area.

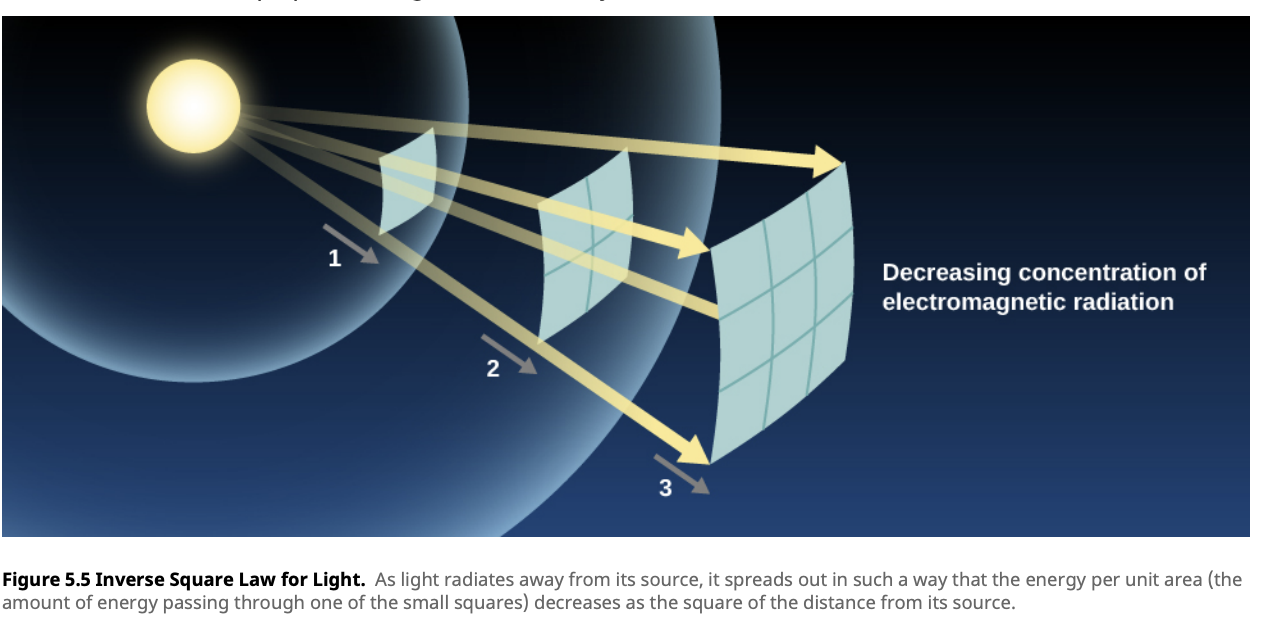
Inverse Square Law

Example: Calculating the Solar Flux at Different Distances

The luminosity of the Sun is $ 3.839 \times 10^{26} $ W and is at a distance of 1 AU (astronomical unit) away from Earth, which is $ 1.496 \times 10^{11} $ meters.

Earth receives a radiant flux above its absorbing atmosphere given by:

\[F = \frac{L}{4\pi r^2}\] \[F = \frac{3.839 \times 10^{26}}{4\pi (1.496 \times 10^{11})^2}\] \[F \approx 1365 \, \text{W/m}^2\]

This value of the solar flux is known as the solar irradiance, sometimes also called the solar constant.

Apparent Brightness and the Magnitude Scale

Apparent Magnitude

The apparent magnitude of a star is a measure of its brightness as seen from Earth. This concept is crucial because it takes into account both the intrinsic luminosity of the star and its distance from us.

Historical Background of the Magnitude Scale

The magnitude scale dates back to the ancient Greek astronomer Hipparchus, who classified stars according to their apparent brightness. This system was refined by Ptolemy and later standardized to a logarithmic scale, where a difference of 5 magnitudes corresponds to a factor of 100 in brightness.

The logarithmic nature of the scale is represented by:

\[m_1 - m_2 = -2.5 \log_{10} \left( \frac{F_1}{F_2} \right)\]

where $ m_1 $ and $ m_2 $ are the magnitudes of two stars, and $ F_1 $ and $ F_2 $ are their respective fluxes.

Another way to write this equation is:

\[\frac{F_2}{F_1} = \left(100^{0.2}\right)^{m_1 - m_2}\]

which allows us to compare the flux of two objects (and the flux is what we would typically call “brightness” in every day conversation).

The star Vega was historically used as the standard for apparent magnitude, set at 0. Modern measurements have slightly adjusted this value, but Vega remains a key reference point in the magnitude system.

Recall: A logarithm is a mathematical operator that tells us the power to which a base number must be raised to obtain a given number. When the base is not specified, it is assumed to be 10.

For example, $ \log_{10}(100) = 2 $ because $ 10^2 = 100 $.

Logarithmic scales are used in astronomy to manage the huge differences in the brightness and distances of celestial objects.

Apparent Magnitudes of Well-Known Objects

Example: Suppose an astronomer has discovered something special about a dim star with a magnitude of 8.5 and wants to explain how much dimmer this star is compared to Sirius. We'll use the dim star as Star 1 and Sirius as Star 2 in our equation.

Given:

Dim star magnitude, $ m_1 = 8.5 $

Sirius magnitude, $ m_2 = -1.5 $

Solution:

\[\frac{F_2}{F_1} = \left(100^{0.2}\right)^{8.5 - (-1.5)}\] \[\frac{F_2}{F_1} = \left(100^{0.2}\right)^{10}\] \[\frac{F_2}{F_1} = (100)^2 = 100 \times 100 = 10,000\]

Therefore, the dim star is 10,000 times dimmer than Sirius.

Example: It is a common misconception that Polaris (magnitude 2.0) is the brightest star in the sky. However, Sirius, with a magnitude of -1.5, holds that title. Let's compare the apparent brightness of Sirius to Polaris.

Given:

Polaris magnitude, $ m_1 = 2.0 $

Sirius magnitude, $ m_2 = -1.5 $

Solution:

\[\frac{F_2}{F_1} = \left(100^{0.2}\right)^{2.0 - (-1.5)}\] \[\frac{F_2}{F_1} = \left(100^{0.2}\right)^{3.5}\] \[\frac{F_2}{F_1} = 100^{0.7} = 25\]

Our calculation shows that Sirius’ apparent brightness is 25 times greater than Polaris’ apparent brightness.

Absolute Magnitude

Absolute magnitude is the apparent magnitude (brightness) a star would have if it were placed at a standard distance of 10 parsecs from Earth. This standardization allows astronomers to compare the true brightness of stars without the confounding effect of distance.

The relationship between a star’s absolute magnitude $ M $, apparent magnitude $ m $, and distance $ d $ in parsecs is given by:

\[M = m + 5 - 5 \log_{10}(d)\]

Distance Modulus

Explanation of Distance Modulus

The distance modulus provides a way to calculate the distance to a star based on its apparent and absolute magnitudes. The formula is:

\[m - M = 5 \log_{10}(d) - 5\]

where:

This equation is incredibly useful for determining stellar distances, making it a cornerstone of astronomical measurement.

Example: Calculating the Absolute Magnitude of the Sun

The apparent magnitude of the Sun, $ m_{\text{Sun}} $, is $ -26.83 $, and its distance from Earth is 1 AU, which is $ 4.848 \times 10^{-6} $ parsecs. Using the formula for absolute magnitude:

\[M_{\text{Sun}} = m_{\text{Sun}} - 5 \log_{10}(d) + 5\]

we can calculate the absolute magnitude of the Sun.

\[M_{\text{Sun}} = m_{\text{Sun}} - 5 \log_{10}(d) + 5\] \[M_{\text{Sun}} = -26.83 - 5 \log_{10}(4.848 \times 10^{-6}) + 5\]

Since $ \log_{10}(4.848 \times 10^{-6}) \approx -5.315 $:

\[M_{\text{Sun}} = -26.83 - 5(-5.315) + 5\] \[M_{\text{Sun}} = -26.83 + 26.575 + 5\] \[M_{\text{Sun}} = 4.74\]

Thus, the absolute magnitude of the Sun is $ +4.74 $.

Check Your Understanding

  1. Brightness: Other than the distance to a star, what characteristics of a star do you think would make it more or less bright to us?

  2. Flux and Luminosity: Given a star with a luminosity of $ 4 \times 10^{26} $ watts and a distance of 2 parsecs, calculate the flux received on Earth.

  3. Magnitude Scale Use the Magnitude Scale equation below to explain why a magnitude 2 compared to a magnitude 5 star is about 16 times brighter.
\[m_1 - m_2 = -2.5 \log_{10} \left( \frac{F_1}{F_2} \right)\]
  1. Absolute Magnitude: If a star has an apparent magnitude of 7 and is located 50 parsecs away, what is its absolute magnitude?

  2. Apparent Brightness: Two stars have apparent magnitudes of 3 and 5. Calculate the ratio of their fluxes (i.e. $\frac{F_2}{F_1}$).

  3. Distance Modulus: Calculate the distance to a star with an apparent magnitude of 10 and an absolute magnitude of 2.

  4. Flux: At what distance from a 100-W light bulb is the radiant flux equal to the solar irradiance?

  5. Algebra Challenge: Derive the relation
\[m = M_{Sun} − 2.5 \log_{10}(\frac{F}{F_{10,Sun}})\]

where $M_{Sun}$ is the absolute magnitude of the Sun and $F_{10,Sun}$ is the flux received from the Sun if it were 10 parsecs away from the observer.

Resources