Introduction

In the winter of 1995, scientists pointed the Hubble Space Telescope at a seemingly empty patch of sky near the Big Dipper. Over ten consecutive days, the telescope took close to 150 hours of exposure of this dark, unobtrusive spot. What came back was nothing short of spectacular: an image of over 1,500 distinct galaxies glimmering in a tiny sliver of the universe. This was just a fraction of the sky, about the size of a ballpoint pen tip held at arm’s length, revealing an incredible truth about the vastness of our cosmos. This lesson will explore the immense scales of the universe, from our solar system to the farthest reaches observed by humanity, illustrating the vast distances and sizes that define our universe.

Scientific Notation

To understand the vast distances and sizes in the universe, we need to use scientific notation. This method allows us to express very large and very small numbers in a manageable way. For example, the distance from the Earth to the Sun is about 150,000,000 kilometers, which can be written as $1.5 \times 10^8$ kilometers.

One way to think of scientific notation is to think of how many digits to you have to move the decimal place (postivie exponents to the right, negative exponents to the left). For example, $3.8 \times 10^{3}=3800$, whereas $3.8 \times 10^{-3}=0.0038$

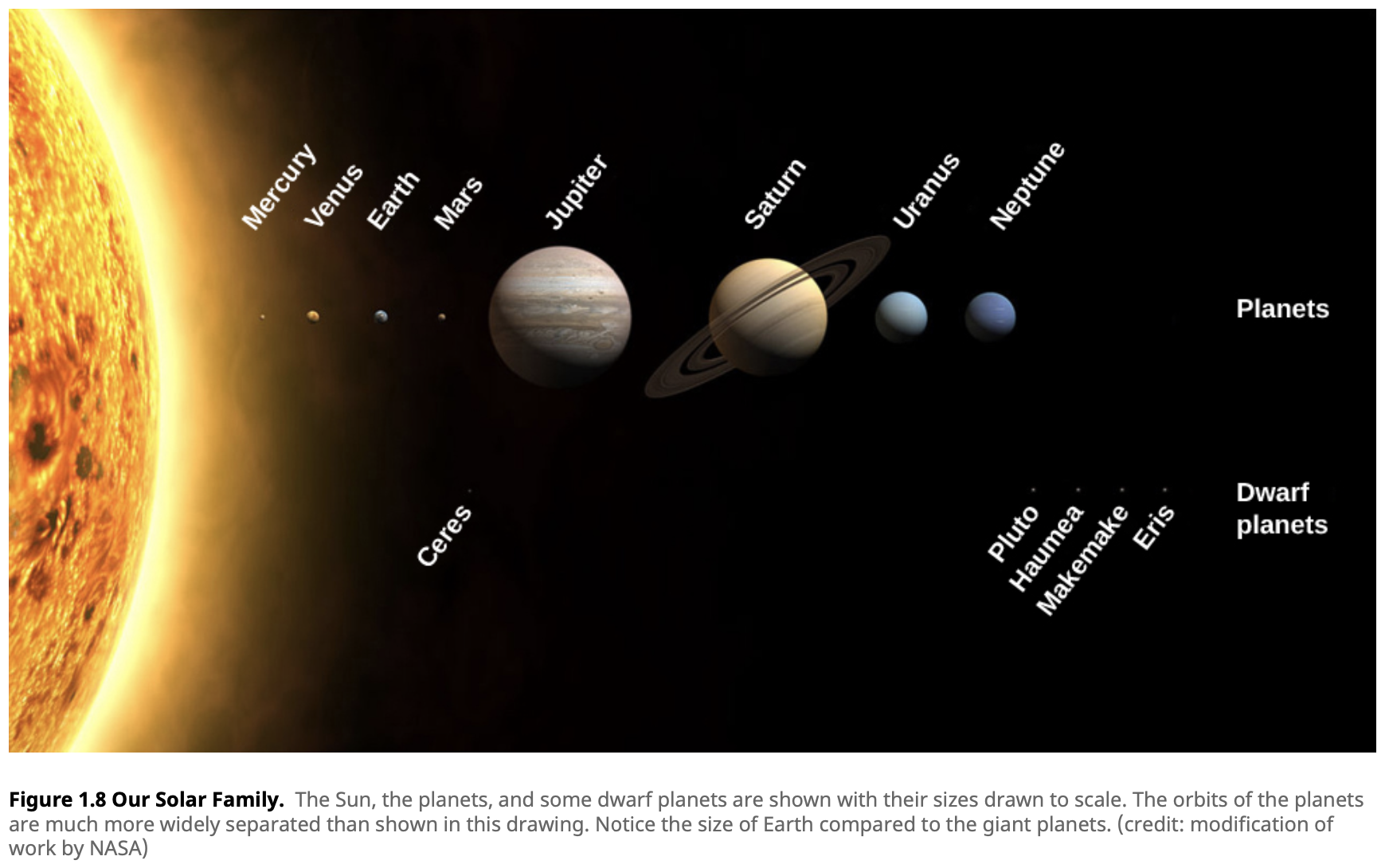
The Size and Scale of the Solar System

The solar system is our cosmic neighborhood, and its scale is immense. The Sun, the central star, has a diameter of about 1.4 million kilometers. Earth, the third planet from the Sun, has a diameter of about 12,700 kilometers. The average distance from Earth to the Sun is approximately 150 million kilometers, also known as 1 Astronomical Unit (AU).

1 Astronomical Unit (AU) is equivalent to $1.496 \times 10^{11}$ meters.

Imagine if the Sun were the size of a basketball. In this model, Earth would be a small apple seed 30 meters away.

Interstellar Distances

Beyond our solar system, the distances between objects become even more staggering. A light-year, the distance light travels in one year, is about 9.46 trillion kilometers. The nearest star to the Sun, Proxima Centauri, is approximately 4.24 light-years away.

Derivation of a Light Year:

Light travels at a speed of approximately 299,792 kilometers per second (km/s) in a vacuum. There are 60 seconds in a minute, 60 minutes in an hour, and 24 hours in a day.

\[\text{Speed of light} = 299,792 \, \text{km/s}\] \[\text{Seconds in a minute} = 60\] \[\text{Minutes in an hour} = 60\] \[\text{Hours in a day} = 24\] \[\text{Days in a year} = 365.25\]

To find the distance light travels in one year:

\[\text{Distance} = \text{Speed} \times \text{Time}\]

First, calculate the number of seconds in a year:

\[60 \times 60 \times 24 \times 365.25 \approx 31,557,600 \, \text{seconds/year}\]

Then, multiply the speed of light by the number of seconds in a year:

\[299,792 \, \text{km/s} \times 31,557,600 \, \text{s/year} \approx 9.46 \times 10^{12} \, \text{kilometers/year}\]

Therefore, one light-year is approximately 9.46 trillion kilometers.

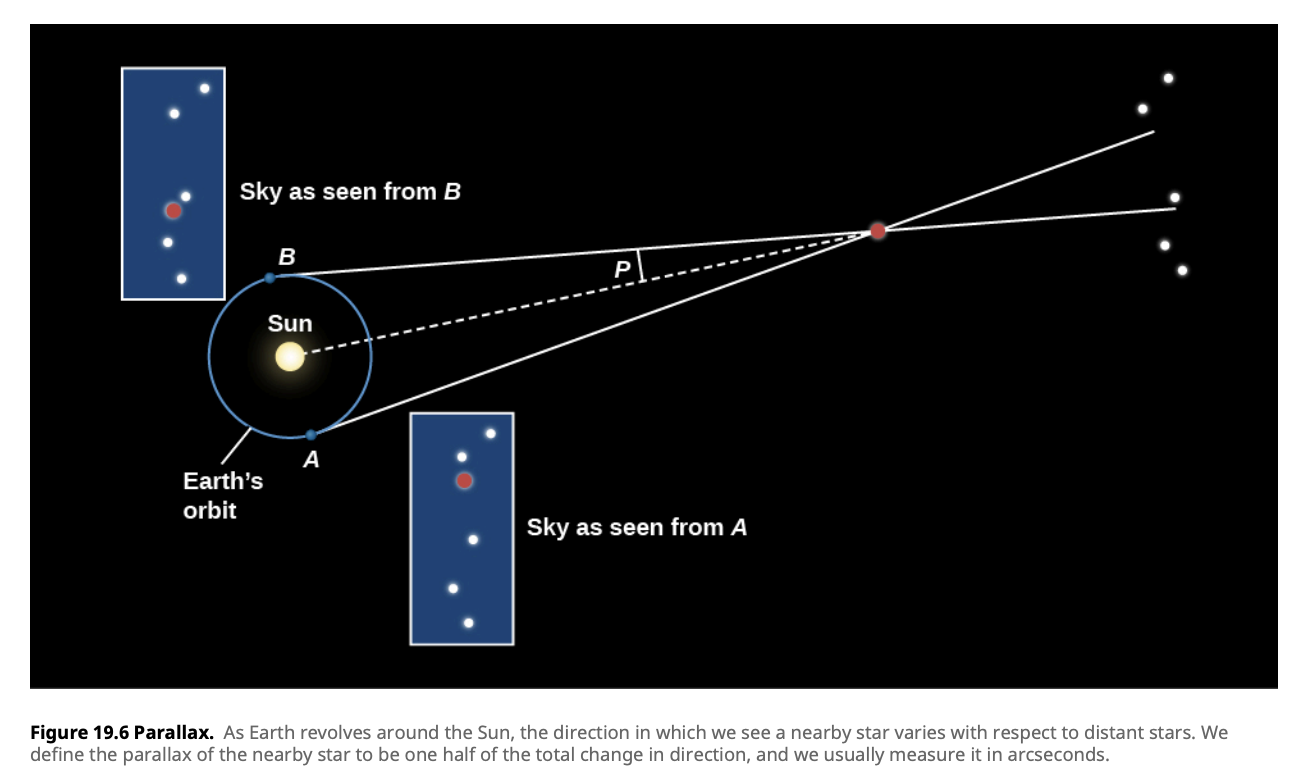
Parallax: Measuring Stellar Distances

Parallax is a method used to measure the distances to nearby stars by observing their apparent movement against the background of more distant stars as Earth orbits the Sun. The parallax angle is half the angle that a star appears to move over six months.

Development of Parallax

The concept of parallax dates back to ancient Greece, where Hipparchus, a Greek astronomer, used it to estimate the distance to the Moon around 150 BCE. Hipparchus observed the apparent shift in the position of the Moon against the background stars when viewed from different locations on Earth. This method relies on the geometric principle that the farther an object is, the smaller its apparent shift when observed from two different points.

However, the method was not applied to stars until the 19th century due to the extremely small angles involved. Friedrich Bessel was the first to successfully measure the parallax of a star, 61 Cygni, in 1838. Bessel’s achievement provided the first direct and reliable measurement of the distance to a star other than the Sun.

What is Parallax?

Parallax is the apparent displacement of an object because of a change in the observer’s point of view. In astronomy, it specifically refers to the apparent shift of a star’s position against the background of distant stars due to Earth’s orbit around the Sun. This shift can be measured at different points in Earth’s orbit, six months apart, to form the maximum parallax angle.

Arcseconds and Parsecs

Arcseconds: When measuring parallax angles, astronomers use very small units called arcseconds. One arcsecond is (1/3600) of a degree. Because the angles involved in stellar parallax are so tiny, using arcseconds allows for more precise measurement.

Parsecs: The distance to a star can be determined using its parallax angle. A parsec (pc) is defined as the distance at which a star would have a parallax angle of one arcsecond. It is derived from the formula:

\[\text{Distance (parsecs)} = \frac{1}{\text{parallax (arcseconds)}}\]

One parsec is approximately equal to 3.26 light-years. This unit of measurement is especially useful in astronomy for calculating vast interstellar distances.

More angle units: In addition to arcseconds, astronomers also use arcminutes and hours to measure angles and time. One arcminute is $\frac{1}{60}$ of a degree, and one hour is $\frac{1}{24}$ of a day.

Using the formula:

\(\text{Distance (parsecs)} = \frac{1}{\text{parallax (arcseconds)}}\) \(\text{Distance} = \frac{1}{0.1} = 10 \text{ parsecs}\)

To convert parsecs to light-years, use the conversion factor: \(1 \text{ parsec} = 3.26 \text{ light-years}\) \(10 \text{ parsecs} = 10 \times 3.26 = 32.6 \text{ light-years}\)

Applications and Limitations

Parallax is a fundamental method for measuring distances to nearby stars within a few hundred light-years from Earth. Beyond this range, the parallax angles become too small to measure accurately with current technology. However, advancements in space telescopes, like the Gaia mission, have significantly increased the precision of parallax measurements, allowing astronomers to map stars up to tens of thousands of light-years away.

The Milky Way Galaxy

The Milky Way is our galaxy, a massive collection of stars, gas, and dust bound together by gravity. It contains between 100 to 400 billion stars, including our Sun. Our solar system is located in one of the spiral arms of the Milky Way, about 27,000 light-years from the galactic center. The Milky Way itself is about 100,000 light-years in diameter.

The Local Group and Other Galaxies

The Milky Way is part of a larger collection of galaxies known as the Local Group, which contains about 54 galaxies. The Andromeda Galaxy, approximately 2.5 million light-years away, is the closest spiral galaxy to the Milky Way. Galaxies come in various shapes and sizes, including spiral, elliptical, and irregular.

Did You Know? The Andromeda Galaxy and the Milky Way are on a collision course and are expected to merge in about 4.5 billion years to form a new galaxy, sometimes dubbed “Milkomeda.”

The Observable Universe

Beyond the Local Group lies the observable universe, a vast expanse containing billions of galaxies. The observable universe is about 93 billion light-years in diameter. Superclusters and voids are large-scale structures within the universe, with superclusters containing thousands of galaxies.

Interesting Side Note: The Hubble Deep Field image, taken in the mid-1990s, revealed over 1,500 galaxies in a tiny area of the sky, approximately one two-millionth of the night sky. This image showed the immense scale and richness of the universe.

Methods of Measurement

In this lesson, we studied the use of parallax to measure interstellar distances.

Astronomers use various other methods to measure distances in the universe, each suited to different scales and types of objects. We will study these more throughout the course.

1. Parallax:
   • Useful For: Measuring distances to nearby stars within a few hundred light-years.
   • How It Works: Observes the apparent movement of a star against the background of more distant stars as Earth orbits the Sun. The parallax angle is half the angle that a star appears to move over six months. This method is most effective for stars relatively close to us.
   • Further Insight: Parallax measurements become increasingly difficult for stars that are farther away due to the very small angles involved. Advanced instruments, such as the Gaia space observatory, have significantly improved the accuracy of parallax measurements, enabling the mapping of stars up to tens of thousands of light-years away.
2. Standard Candles:
   • Useful For: Measuring distances to stars and galaxies up to tens of millions of light-years away.
   • How It Works: Uses objects with known luminosity, such as Cepheid variables and Type Ia supernovae, to determine distance based on their observed brightness. By comparing the known intrinsic brightness with the observed brightness, the distance to the object can be calculated.
   • Further Insight: Cepheid variables have a well-defined relationship between their luminosity and pulsation period, making them reliable distance indicators. Type Ia supernovae, known for their consistent peak brightness, are used to measure distances to faraway galaxies.
3. Redshift:
   • Useful For: Measuring distances to very distant galaxies and the overall scale of the universe.
   • How It Works: Measures the shift in the spectral lines of distant galaxies toward the red end of the spectrum. This redshift is due to the expansion of the universe and can be used to determine the galaxy’s distance. The greater the redshift, the farther away the galaxy is.
   • Further Insight: Redshift measurements are fundamental to cosmology, providing crucial data for understanding the expansion rate of the universe (Hubble’s Law) and the distribution of galaxies on a large scale.

Check Your Understanding

1. Unit Conversion: The distance from Earth to Proxima Centauri is 4.24 light-years. Convert this distance to km, using appropriate scientific notation. How many Astonomical Units (AUs) would this be?
   
   

2. Speed of light: The distance from Earth to the Sun is 149 million kilometers. How long does it take the light from the Sun to reach Earth’s surface?
   
   

3. Solar System Scale: If the Sun were the size of a basketball, how far would Neptune be in your model?
   
   

4. Parallax: Explain how parallax is used to measure the distance to nearby stars.
   
   

5. Measuring Distances: If a star has a parallax angle of 0.23 arcseconds, what is its distance from Earth in parsecs? Convert this distance to light-years and kilometers (using scientific notation).
   
   

Resources

• Astronomy (2016). Andrew Fraknoi, David Morrison, and Sidney C. Wolff.